信息导论笔记，斜体部分了解即可

Chapter 1 离散信源与信息熵

概述：本章知识结构可以大致概括为：

1.信息

2.单符号离散信源

3.信息量

4.熵以及熵的性质

信息

信息定义很多，不多做赘述。

就本科目所学知识而言，信息是对不确定性的描述，不确定的东西才有研究的价值，延伸至其他领域，随机变量这一研究对象则很符合这样的“不确定性”，所以我们可以理解为信息是对随机变量不确定性的描述。

通信系统的基本模型为：信源→信源编码→加密→信道编码→信道→信道译码→解密→信源译码→信宿

我们所研究的内容以最基础的简单通信系统为例即可：

信源→信道→信宿

信源是通信系统的发射端。

信宿是通信系统的接收端。

消息是信息的载体。

信源是随机的，

信道的影响是随机的，信宿也就是随机的。

之后的内容基本上就围绕上述模型展开进行研究。

主要以香农信息论为主。

信源

前言

既然需要研究信源，则首先需要理解我们研究信源特性的动机：

※提高信源效率，尽可能使其适用于传输

※进行编码，以便“一切尽在不言中”（老师PPT里的原话，不明白啥意思😋😋😋）

信源的分类

✧离散/连续（数字/模拟）——根据信源的时间、相位、频率、幅度分布特性

✧二进制/多进制 —— 根据数字信源的消息集合大小

✧无记忆/有记忆 —— 离散信源产生的消息序列的内部关联性

✧离散/连续 & 平稳/非平稳 —— 离散信源的随机过程

单符号离散信源☜☜☜

如果信源每次发出的消息都是单一符号，而这些符号的取值是有限或可数的，则称这种信源为单符号离散信源。(e.g. 扔骰子、普通的天气气象)

以扔骰子为例，我们可以将这一单符号离散信源表示为：
$$
\left[ \begin{array}{c}X \\ P(X)\end{array}
\right]=\left[\begin{array}{c} 1 &2 &3 &4 &5 & 6 \\ \frac{1}{6} & \frac{1}{6}& \frac{1}{6}& \frac{1}{6}& \frac{1}{6}&\frac{1}{6}\end{array}\right]
$$
进行广义上的定义如下：
$$
\left[\begin{matrix}X \\ P(X)\end{matrix}\right]=\left[\begin{matrix} x_{1} &x_{2} &x_{3} &… & x_{n} \\ P(x_{1}) & P(x_{2})& P(x_{3})& … &P(x_{n})\end{matrix}\right]
$$
(注：此处需要概率论知识：①联合概率；②条件概率)

自信息量☜☜☜

此处有关自信息量定义过程稍微有点冗杂（其实是笔者太懒不想看），可以这样理解：消息中包含的不确定性的成分是信息，不确定性的成分越大（出现的概率越小），信息量就越大，之后我们便可以考虑这个量是多少，应该如何表示了。

基于离散信源，$x_{i}$ 所包含的信息量为$I(x_{i})$ ，其需要满足如下条件（为什么要满足这些条件我也不太清楚）：

①$I(x_{i})$与$x_{i}$的概率$P(x_{i})$相关

②$I(x_{i})$是$P(x_{i})$的连续函数

③$I(x_{i})$是$P(x_{i})$的减函数，且当$P(x_{i})$=1时$I(x_{i})$=0

对以上条件进行数学建模，可以得到自信息量的定义为：
$$
I(x_{i})=-log_xP(x_{i})
$$
根据对数底数的不同，自信息量的单位不同：

2——比特（bit）

e——奈特（nat）

10——哈特（Hart）

目前的通信系统或其他信息传输系统大多以二进制为基础，因此信息量的单位以bit 最为常用。即：
$$
I(x_{i})=-log_2P(x_{i})=-lbP(x_{i})
$$
注：此处 lb的写法是log binary

其性质按照普通对数函数结合$P(x_{i})$的性质取值特征进行讨论即可，不多做赘述。

互信息量

之后讨论，此处不多做赘述😏😏😏。

信息熵☜☜☜

一个单符号离散信源发出的各种消息——自信息量

该信源整体的信息量如何度量——？？？

引入信息熵，其定义为：

$H(X)=E[I(x_{i})]=\sum_{i=1}^{n}P(x_{i})I(x_{i})=-\sum_{i=1}^{n}P(x_{i})lbP(x_{i})$

可以从统计的角度出发：根据概率论的知识可知：数学期望反映了随机变量的统计特性，类比至信息量与信息熵即可理解

◼信源熵H(X)表示信源输出后，平均每个离散消息所提供的信息量。

◼ 信源熵H(X)表示信源输出前，信源的平均不确定度。

◼ 信源熵H(X)反映了变量X的随机性。

信息熵的单位为：比特/符号（bit/symbol）

其性质有：非负性、严格上凸性、最大熵定理

最大熵定理为(证明过程略，但是比较重要)：
$$
H(X)\le lb(n) \enspace\enspace or\enspace\enspace H(X)\le log_{2}n
$$

多符号离散信源☜☜☜

定义如下：如果任何时刻信源发出的消息都是有限或可数的符号序列，而每个符号都取值于同一个有限或可数的集合，则称这种信源为多符号离散信源。

(e.g. 掷多个色子，再比如发短消息，每条短消息只包含多个字)

多符号（N）离散信源发出的符号序列记为
$$
X_{1}X_{2}X_{3}…X_{N}
$$
序列中的任一符号取值于集合：
$$
X_{k}\in { x_{1} , x_{2},…,x_{n} }, k=1, 2, …
$$

二维离散平稳信源

数学模型为：
$$
\left[\begin{matrix}X_{1}X_{2} \\ P(X_{1}X_{2})\end{matrix}\right]=\left[\begin{matrix} a_{1} &a_{2} &… & a_{n^{2}} \\ P(a_{1}) & P(a_{2}) & … &P(a_{n^{2}})\end{matrix}\right]
$$
信息熵为：
$$
H(X_{1}X_{2})=-\sum_{i=1}^{n^{2}}P(a_{i})lbP(a_{i})
$$
中间有一段推导过程，此处省略，最终可以得到：
$$
H(X_{1}X_{2})=H(X_{1})+H(X_{2}/X_{1})
$$
其中：

$H(X_{1})、H(X_{2})$ → 无条件熵

$H(X_{1}X_{2})$ → 联合熵

$H(X_{2}/X_{1})$ → 条件熵

通过数学方法可以证明：
$$
H(X_{1}X_{2}) \le H(X_{1})+H(X_{2})=2H(x_{1})
$$
如果将该信源符号所提供的平均信息量记为$H_{2}(X_{1}X_{2})$并称其为平均符号熵，也叫熵率，则:
$$
H_{2}(X_{1}X_{2}) = \frac{1}{2}H(X_{1}X_{2}) \le H(x_{1})
$$

多符号离散平稳信源

对于多符号离散信源发出的符号序列：
$$
X_{1}X_{2}X_{3}…X_{N}
$$
如果有两个不同的时刻k和l，其中
$$
k=1, 2, … \enspace\enspace\enspace l=1, 2, …
$$
且概率分布相同，即：
$$
P(X_{k})=P(X_{l})
$$
则称该多符号离散信源为一维离散平稳信源

同时如果其二维联合概率分布也相同，即
$$
P(X_{k})=P(X_{l}) \\
P(X_{k}X_{k+1})=P(X_{l}X_{l+1})
$$
则称该多符号离散信源为二维离散平稳信源

拓展到N维：
$$
P(X_{k})=P(X_{l}) \\
P(X_{k}X_{k+1})=P(X_{l}X_{l+1}) \\
… \\
P(X_{k}X_{k+1}…X_{k+N-1})=P(X_{l}X_{l+1}…X_{l+N-1})
$$
则称该多符号离散信源为N维离散平稳信源

注意：直到N维的各维联合概率分布都与时间起点无关。

由此得到其数学模型：
$$
\left[\begin{matrix}X_{1}X_{2}…X_{N} \\ P(X_{1}X_{2}…X_{N})\end{matrix}\right]=\left[\begin{matrix} a_{1} &a_{2} &… & a_{n^{N}} \\ P(a_{1}) & P(a_{2}) & … &P(a_{n^{N}})\end{matrix}\right]
$$
其中，
$$
a_{i}=x_{i_{1}}x_{i_{2}}…x_{i_{N}} \\
P(a_{i}) =P(x_{i_{1}}x_{i_{2}}…x_{i_{N}})=P(x_{i_{1}})P(x_{i_{2}}/x_{i_{1}})P(x_{i_{N}}/x_{i_{1}}x_{i_{2}}…x_{i_{N-1}})
$$

多符号离散平稳信源的信息熵

联合自信息量:
$$
I(a_{i})=I(x_{i_{1}},x_{i_{2}},..,x_{i_{N}})=-lbP(x_{i_{1}},x_{i_{2}},..,x_{i_{N}})
$$
条件信息量：
$$
I(x_{i_{N}}/x_{i_{1}},..,x_{i_{N-1}})=-lbP(x_{i_{N}}/x_{i_{1}},..,x_{i_{N-1}})
$$
信息熵：
$$
H(X_{1}X_{2}…X_{N})=H(X_{1})+H(X_{2}/X_{1})+…+H(X_{N}/X_{1}X_{2}…X_{N-1})
$$

$$
H(X_{1}X_{2}…X_{N})=\frac{1}{N}H(X_{1}X_{2}…X_{N}) \le H(X_{1})
$$

当$N→\infty$时，平均符号熵取极限值，成为极限熵：
$$
H_{\infty}=\lim_{N→\infty}H(X_{1}X_{2}…X_{N})/N=\lim_{N→\infty}H(X_{N}/X_{1}X_{2}…X_{N-1})
$$

多符号离散平稳无记忆信源

如果离散平稳信源发出的符号序列中各符号相互独立，则称该信源为**离散平稳无记忆信源**。

根据N维离散平稳信源数学模型：
$$
\left[\begin{matrix}X_{1}X_{2}…X_{N} \\ P(X_{1}X_{2}…X_{N})\end{matrix}\right]=\left[\begin{matrix} a_{1} &a_{2} &… & a_{n^{N}} \\ P(a_{1}) & P(a_{2}) & … &P(a_{n^{N}})\end{matrix}\right]
$$
其中，
$$
a_{i}=x_{i_{1}}x_{i_{2}}…x_{i_{N}} \\
$$

$$
P(a_{i}) =P(x_{i_{1}}x_{i_{2}}…x_{i_{N}})=P(x_{i_{1}})P(x_{i_{2}}/x_{i_{1}})P(x_{i_{N}}/x_{i_{1}}x_{i_{2}}…x_{i_{N-1}})
$$

如果各个符号相互独立，则有：
$$
P(a_{i}) =P(x_{i_{1}}x_{i_{2}}…x_{i_{N}})=P(x_{i_{1}})P(x_{i_{2}})…P(x_{i_{N}})
$$
相当于一维离散平稳信源扩展N次，也叫N次扩展信源。

由此我们可以得到N维离散平稳无记忆信源数学模型：
$$
\left[\begin{matrix}X^{N} \\ P(X^{N})\end{matrix}\right]=\left[\begin{matrix} a_{1} &a_{2} &… & a_{n^{N}} \\ P(a_{1}) & P(a_{2}) & … &P(a_{n^{N}})\end{matrix}\right]
$$

$$
P(a_{i}) =P(x_{i_{1}}x_{i_{2}}…x_{i_{N}})=P(x_{i_{1}})P(x_{i_{2}})…P(x_{i_{N}})
$$

信息熵：
$$
H(X^{N})=H(X_{1})+H(X_{2})+…+H(X_{N})=NH(X_{1})
$$
平均符号熵：
$$
H_{N}(X^{N})=\frac{1}{N}(X_{N})=H(X_{1})
$$
极限熵：
$$
H_{\infty}=\lim_{N→\infty}\frac{1}{N}H(X_{N})=\lim_{N→\infty}H(X_{1})=H(X_{1})
$$

马尔科夫（Markov）信源

如果离散平稳信源发出的符号只与前面已经发出的m(<N)个符号相关，则称该信源为m阶马尔科夫信源。

马尔科夫信源是离散平稳有限记忆信源，马尔科夫信源的记忆长度为 m 。

它产生的符号序列的符号之间有相关性。

数学模型为：
$$
\left[\begin{matrix}X_{m+1}/X_{1}X_{2}…X_{N} \\ P(X_{m+1}/X_{1}X_{2}…X_{N})\end{matrix}\right]=\left[\begin{matrix} a_{1} &a_{2} &… & a_{n^{m+1}} \\ P(a_{1}) & P(a_{2}) & … &P(a_{n^{m+1}})\end{matrix}\right]
$$
其中，
$$
a_{i}=x_{i_{m+1}}/x_{i_{1}}x_{i_{2}}…x_{i_{N}} \\
$$

$$
P(a_{i}) =P(x_{i_{m+1}}/x_{i_{1}}x_{i_{2}}…x_{i_{m}})
$$

引入状态序列，其数学模型可以描述为：
$$
\left[\begin{matrix}S_{m+1}/S_{m} \\ P(S_{m+1}/S_{m})\end{matrix}\right]=\left[\begin{matrix} e_{1}/e_{1} &e_{2}/e_{1} &… & e_{n^{m}-1}/e_{n^{m}}&e_{n^{m}}/e_{n^{m}} \\ P(e_{1}/e_{1}) & P(e_{2}/e_{1}) & … &P(e_{n^{m}-1}/e_{n^{m}})&e_{n^{m}}/e_{n^{m}}\end{matrix}\right]
$$
且
$$
\sum_{j=1}^{n}P(e_{j}/e_{i})=1
$$
此类例题一般使用状态转移图解决！！！

极限熵：
$$
H_{\infty}=H_{m+1}=-\sum_{i=1}^{n^{m}}\sum_{j=1}^{n^{m}}P(e^{i})P(e^{j}/e^{i})lbP(e^{j}/e^{i})
$$

信息冗余度——懒了没看

信源符号序列分组定理——懒了没看

无失真编码定理——懒了没看

Chapter 2 无失真信源编码

前言

信息传输的3个关键要求——**效率、可靠、安全**。

信源编码：为了满足信道特性，往往需要**将n元的信源符号序列变换为m元(一般为二元)** 的信源码序列的过程。

无失真——编码和译码过程中不丢失信息。

无失真信源编码

保证符号元与码字一一对应，此时用码序列表示的信源信息熵保持不变。

例题：
$$
\left[ \begin{array}{c}X \\ P(X)\end{array}
\right]=\left[\begin{array}{c} x_{1} &x_{2} &x_{3} &x_{4} \\ 0.5{6}& 0.3& 0.15&0.05\end{array}\right]
$$
最简单的无失真编码：4–2进制变换
$$
x_{1}→00， x_{2}→01，x_{3}→10，x_{4}→11
$$
编码的码长K=2,其编码效率为：
$$
\eta=\frac{H(X)}{K}\approx 82.4%
$$
考虑到编码效率，此时考虑压缩比特数，进行不等长编码，即（注：下方法无法实现无失真译码）：
$$
x_{1}→0， x_{2}→1，x_{3}→00，x_{4}→01
$$
此时一种保证符号元与码字一一对应的不等长编码为：
$$
x_{1}→0， x_{2}→10，x_{3}→110，x_{4}→111
$$
编码的码长：
$$
\overline{K} =0.5\times 1+0.32\times 2+0.15\times3+0.05\times 2=1.7
$$
其编码效率为：
$$
\eta=\frac{H(X)}{K}\approx 96.9%
$$

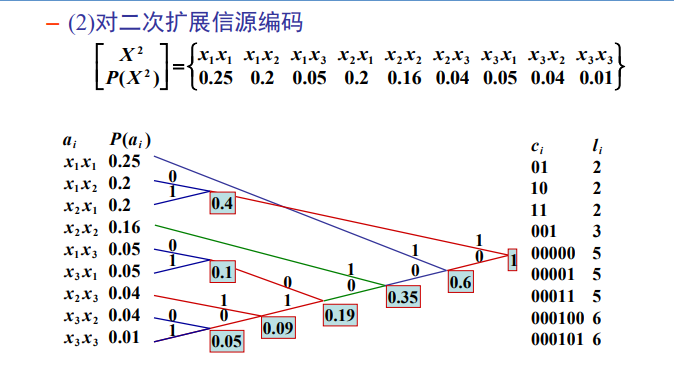
信源二次扩展

将信源进行二维拓展组合即可。

一些小结论：
①不等长编码的平均码长可以是小数比特。

②大概率符号序列编为短码、小概率符号序列编为长码有助于压缩平均码长。

③ 信源的N次扩展有助于压缩平均码长，随N的增大，可以预见码率可能渐进达到信源编码的下界。

④出现无失真译码问题——由于码长不等，接收端如何从码序列串中唯一分割出对应与每一个符号序列的码字。

无失真编码定理

一些概念

如果所采用的不等长编码使接收端能从码序列中唯一地分割出对应与每一个符号元的码字，则称该不等长编码为单义可译码。

单义可译码中，如果能在对应于每一个符号元的码字结束时立即译出的称为即时码，如果要等到对应与下一个符号元的码字才能译出的称为延时码。

e.g.
$$
A:0 , 1, 00, 01 \\
B:0, 01, 011, 0111 \\
C:0, 10, 110, 111
$$
A不是单义可译码，有二义性

B是延时码

C是即时码

~~而考试没有码~~

码数图

类比二叉树，不多做赘述

克拉夫特（Kraft）不等式

m元长度为$k_{i}, i=1, 2, …, n$的异前置码存在的充分必要条件是：
$$
\sum_{i=1}^{n}m^{-k_{i}} \le 1
$$
可以这样理解，取m=2，先选取0作为其中一个码字，因为Kraft不等式表示的编码方式中每个码字长度不定，因此，每个码字不能是另一个码字的前缀。所以，当我们选取0作为一个码字后，我们就不能再将一个以0开头的二进制串作为码字。

无失真编码定理

如果$N$维离散平稳信源的平均符号熵为$H_{N}(X_{1}X_{2}…X_{N})$，对信源符号序列进行m元不等长组编码，一定存在一种无失真编码方法，当$N$足够大时，使得每个信源符号序列所对应码字的平均比特数：
$$
H_{N}(X_{1}X_{2}…X_{N}) \le \frac{\overline{K}}{N}lb \le H_{N}(X_{1}X_{2}…X_{N}) +\varepsilon
$$
$\varepsilon $为任意给定的小正数。

证明过程略

香农编码

香农编码的编码步骤如下：
①将符号元$x_{i}$按概率进行降序排列；

②令$p(x_{0})=0$，计算第$i$个码字的累加概率：
$$
p_{a}(x_{i})=\sum_{j=0}^{i-1}p(x_{j}),i=1, 2,…, n
$$
**③确定第$i$个码字的码长$**k_{i}$
$$
-lbp(x_{i}) \le k_{i} <-lbp(x_{i})+1
$$
④将$p_{a}(x_{i})$用二进制表示，取小数点后$k_{i}$位作为符号元$x_{i}$的码字

霍夫曼(Huffman)编码

霍夫曼(Huffman)编码的编码步骤如下（其效率高于香农编码）：

①将符号元$x_{i}$按概率进行降序排列；

②为概率最小的符号元分配一个码元1，概率次小的符号元分配一个码元0；

③将概率最小的两个符号元合并成一个新的符号元，用两者概率之和作为该新符号元的概率；

④重复以上三个步骤，直到最后合并出一个以1为概率的符号元，结束编码。

e.g.

Chapter 3 离散信道与信道容量

互信息量

互信息量是一个随机变量包含另-个随机变量的信息量

或通过一个随机变量获取另一个随机变量所具有的信息量

它反映的也是两个随机变量间的关系；

考虑到最简单的通信系统：

信源→信道→信宿

设单符号离散信源：
$$
\left[\begin{matrix}X \\ P(X)\end{matrix}\right]=\left[\begin{matrix} x_{1} &x_{2} &… & x_{n} \\ P(x_{1}) & P(x_{2})& … &P(x_{n})\end{matrix}\right]
$$
单符号离散信宿：
$$
\left[\begin{matrix}Y \\ P(X)\end{matrix}\right]=\left[\begin{matrix} y_{1} &y_{2} &… & y_{n} \\ P(y_{1}) & P(y_{2})& … &P(y_{n})\end{matrix}\right]
$$
☻如果是无噪信道，当信源发出x，信宿接收到的也必是x，因此，信道的输出y就等于输入x。

☻如果是有噪信道，信号通过信道就会产生失真，此时，信道的输出y一般不等于输入x，但它们之间会满足一定关系，由于噪声的随机性，用条件概率来描述这种关系是恰当的。

故**单符号离散信道的数学模型**可以表示为：

$$
P(Y/X)=\left[\begin{matrix} p(y_{1}/x_{1}) &p(y_{2}/x_{1}) &… &p(y_{m}/x_{1})\\ p(y_{1}/x_{2}) & p(y_{2}/x_{2})& … &p(y_{m}/x_{2})\\
…& …& …& …
\\
p(y_{1}/x_{n}) & p(y_{2}/x_{n})& … &p(y_{m}/x_{n})
\end{matrix}\right]
$$

信源发出$x_{i}$，信宿接收$y_{j}$，所包含的信息量用$I(y_{j};x_{i})$表示，我们称为$x_{i}$对$y_{j}$的互信息量(单位为bit)。

数学关系如下：
$$
I(y_{j};x_{i})=I(y_{j})-I(y_{j}/x_{i})=-lbP(y_{j})+lbP(y_{j}/x_{i})=lb\frac{P(y_{j}/x_{i})}{P(y_{j})}
$$
其性质略。

无噪信道和信道中断的情况显而易见，不多做赘述。

please温习概率论当中的边缘分布知识

平均互信息量

如果将离散信道所有x对y的互信息量在联合概率空间$p(x_{i}y_{j})$的数学期望用$I(Y;X)$来表示并称其为X对Y的平均互信息量，则平均互信息量的定义为：
$$
I(Y;X)=\sum_{i=1}^{n}\sum_{j=1}^{m}p(x_{i}y_{j})I(y_{j};x_{i})=\sum_{i=1}^{n}\sum_{j=1}^{m}p(x_{i}y_{j})lb\frac{p(y_{j}/x_{i})}{p(y_{j}}
$$
平均互信息量也称为交互熵，单位为bit/symbol。

以信源作为参考：
$$
I(Y;X)=H(X)-H(Y/X)
$$
此时的条件熵$H(Y/X)$称为损失熵，是信道给出的平均“信息”量，也称为信道疑义度。

以信宿作为参考：
$$
I(Y;X)=H(Y)-H(Y/X)
$$
此时的条件熵$H(Y/X)$称为噪声熵，是信道给出的平均“信息”量

以系统作为参考：
$$
I(Y;X)=H(X)+H(Y)-H(XY)
$$

性质略，但是很重要。

~~太懒了~~

注意p-I(X;Y)与q-I(X;Y)曲线的绘制

我们可以将平均互信息量理解为信道的信息传输率（不是信息传输速率）。

信道容量

定义

定义：信道转移概率分布P(Y/X)不变时，**平均互信息的最大值为信道容量**，用C表示。
$$
C=\underset{P(X)}\max I(X;Y)
$$
其中P(X)为使I(X;Y)最大的信源概率分布。

单位是bit/symbol

顺水推舟，定义最大的信息传输速率为：
$$
C_{t}=\frac{1}{t}\underset{P(X)}\max I(X;Y)
$$
单位是bit/sec

~~拉格朗日极值方法计算信道容量的过程略。~~

计算步骤

①由
$$
\sum_{j=1}^{m}P(y_{j}/x_{k})\beta_{j}=\sum_{j=1}^{m}P(y_{j}/x_{k})lbP(y_{j}/x_{k})
$$
求出$\beta_{j}$，$k=1, 2, …, n$

②求出：
$$
C=lb(\sum_{j=1}^{m}2^{\beta_{j}})
$$
③求出：
$$
P(y_{j})=2^{\beta_{j}-C}
$$
④由
$$
P(y_{j})=\sum_{i=1}^{n}P(x_{i})P(y_{j}/x_{i})
$$
求出$P(x_{k})$，$k=1, 2, …, n$

均匀信道的信道容量

很重要。

对称信道的信道容量

Very important.

单符号离散信道的信道容量

とても重要です。

多符号离散信道的信道容量

Molto importante.

离散无记忆信道的信道容量

Очень важно.

Chapter 4 信道编码

前言

🥴怎样通过编码，使在信道中传输的消息发生的错误减少到可以接受的程度，进而能否实现无错误传输？🥴

纠错编码的基本思路

一个BSC的例子

设计译码规则A、B

分别求解平均错误概率

发现错误概率既与信道特性有关也与译码规则有关，故称为**译码错误概率**。

所以译码规则的设计应该依据最小错误概率准则进行。

~~u1s1，懒得不想看这个思路，他妈的，考试时间紧张，不多做赘述。~~🤡

信道编码定理

对于离散无记忆信道，如其信道容量为 C，只要信息传输率R<C，一定存在一种编码，当N足够大时，使得译码错误概率$P_{e}$< ε，其中ε为任意给定的小正数.

信道编码定理指出，信道容量C是一个界限，如果信息传输率超过此界限就会出错。

但是信道编码定理没有给出编制纠错码的方法，于是就需要进行后续的讨论。

这是一个有关分类的导引

根据**纠错方式**分类：

✂检错重发（Auto Retransmission with Request, ARQ）

✂前向纠错（Forward Error Correction, FEC）

✂混合纠错 (Hybrid Error Correction, HEC)

根据**纠错码**分类：

⚔线性分组码（汉明码属于线性分组码）

⚔卷积码

⚔Turbo码

⚔LDPC码

⚔ Polar码

其中线性分组码表示为（n,k）

n为码字长度

k为信息位长度

n-k为校验位长度

这是一些重要概念的介绍

码距（汉明距离）

在$m=2^{k}$个码字构成的码中，两个长度为n的码字之间的汉明距离(码距)是指两个码字对应位置上不同码元的个数(其实就是数俩码字之间有多少码元不一样)。

以二元码为例，码距可表示为：
$$
d(c_{i},d_{j})=\sum_{k=1}^{n}c_{i_{k}}\oplus c_{j_{k}}
$$
其中
$$
i,j=1, 2, …, m 且i\ne j
$$
e.g.(1)

$$
c_{1}=1310120 \\
c_{2}=1220310 \\
d(c_{1}, c_{2})=3
$$

最小码距

在m个码字构成的码中，任意两个码字之间码距的最小值称为该码的最小距离。

编码原则是要保证最小码距足够大

错误图案

略

联合渐进均分性定理

略

费诺不等式

略

线性分组码

定义

针对码字个数为$2^k$，码字长度为$n$的码组，若这$2^k$个码字是GF(2)上n维矢量空间的一个k维子空间时，称为(n,k)线性分组码，简称(n,k)码。

定义码率为：$R=K/n$

请复习线性代数向量空间的知识！！！

可参考：信道编码系列(四)：线性分组码(Linear Block code)基础 - 知乎 (zhihu.com)

系统码

如果码字有两部分组成：

第一部分与输入信息序列相同(称为信息位)

第二部分为校验位

具有这个结构的码字称为系统码

线性分组码——编码

输入k位信息：
$$
\mathbf{u}=[u_1, u_2, …, u_k]
$$
输入n长码字：
$$
\mathbf{c}=[c_1, c_2, …, c_k]
$$
规定生成矩阵：
$$
G=\left[\begin{matrix}\mathbf{g_1} \\\mathbf{g_2}\\
:\\\mathbf{g_k}
\end{matrix}\right]=
\left[\begin{matrix} g_{11} &g_{12} &… &g_{1n}\\ g_{21} & g_{22}& … &g_{2n}\\
…& …& …& …
\\
g_{k1} & g_{k2}& … &g_{kn}
\end{matrix}\right]
$$
此时，有编码码字：
$$
\mathbf{c}=\mathbf{u}\mathbf{G}
$$
即：
$$
\mathbf{c}=u_1\mathbf{g_1}+u_2\mathbf{g_2}+…+u_k\mathbf{g_k}
$$
码字是

线性无关矢量的线性组合

线性分组码——译码

接收码字矢量：$\mathbf{r}$

校验矩阵：$\mathbf{H}, \mathbf{GH^{T}=0}$

伴随式矢量：$\mathbf{s}= \mathbf{rH^{T}=(c+e)H^{T}=eH^{T}}$

校验：$\mathbf{s}=0$无误，否则有误

纠错：$\mathbf{s}$只和所接受的误码的错误图案有关且一一对应，
$$
\mathbf{c=r+e}
$$

Chapter 5 连续信源

定义

如果任何是颗信源发出的消息都是单一符号，二这些服啊后的取值是连续的，则该信源位单符号连续信源。

时不变连续信源的数学模型位：
$$
\left[\begin{matrix}X\\ P(X)\end{matrix}\right]=\left[\begin{matrix} a\le x\le b \\ p(x)\end{matrix}\right]
$$
其中p(x)为概率密度函数，满足积分为1的条件.

连续信源熵（绝对熵）

$$
H(X)=-\int_{a}^{b}lbp(x)dx-\lim_{n→\infty}lb\Delta x
$$

微分熵（相对熵）

$$
H_{c}(X)=-\int_{a}^{b}p(x)lbp(x)dx
$$

均匀分布连续信源的相对熵

高斯分布连续信源的相对熵

指数分布连续信源的相对熵

相对熵的性质

可加性

不具有非负性

最大相对熵定理

Chapter 6 连续信道

定义

对应于时不变连续信源和时不变连续信宿的信道为时不变连续信道。

数学模型如下：
$$
X→[P(y/x)]→Y
$$

高斯信道

定义

高斯信道的信道容量

高斯信道的最大信息传输速率

Chapter 7 信息率失真理论

太累了写不下去了，有空了会完善的。